概念梳理汇总
-
集中参数电路 只含集中参数元件的电路(简单来说无需考虑电磁量空间分布)
-
支路 二端元件(两个节点之间)
-
节点 若干支路的连接点(3+)
-
网孔(内网孔) 内部不存在任何支路
-
短路 无论电流为任何有限值电压始终为零的支路
-
开路/断路 无论电压为任何有限值电流始终为零的支路
-
直流电路 由直流电压源或直流电流源激励,且各部分电压和电流都是恒定量的电路
-
线性直流电路 由线性元件和独立源组成的直流电路
线性受控电源应当算作线性元件
基尔霍夫定律
又称电路结构约束
作用范围:集中参数电路
基尔霍夫电流定律(Kirchhoff’s Current Law, KCL)
定律形式和推广形式
- 在集中参数电路中,任一时刻流出(或流入)任一节点的支路电路代数和等于零
- 在集中参数电路中任一时刻流出(或流入)任意闭合边界的支路电流代数和为零
- 在集中参数电路中,任一时刻流出任一节点(或闭合边界)的电流的代数和等于流入该节点(或闭合边界)的电流的代数和
$$\sum i_{流出}=\sum i_{流入} $$
在有 $n$ 个节点的电路中,任意 $n-1$ 个节点的 KCL 方程是一组独立方程
基尔霍夫电压定律(Kirchhoff’s Voltage Law, KVL)
定律形式和推广形式
- 在集中参数电路中,任一时刻沿任一回路各支路电压的代数和等于零
- 在集中参数电路中,沿任一回路,各支路电压降的代数和等于电压升的的代数和
- 在集中参数电路中,任意两点之间的电压具有确定值,与计算路径无关
$$\sum u_{电压降}=\sum u_{电压升} $$
任一回路的 KVL 方程是组成该回路的各个网孔上 KVL 方程的代数和
平面电路网孔上的 KVL 方程是一组独立方程
设电路有 $b$ 个支路 $n$ 个节点,可以证明:平面电路的网孔数即独立 KVL 方程的个数为 $b-n+1$
电路分析
这些电路分析方法都是为了确定电路中的参数
给定的线性直流电路具有 $b$ 条支路,$n$ 个节点
支路电流法(branch current analysis)
以 $b$ 条未知的支路电流作为待求量,对 $n-1$ 个节点列出独立的 KCL 方程,再对 $b-n+1$ 个回路列出独立的 KVL 方程,这 $b$ 个方程联立即可解得 $b$ 个支路电流
要列出 $b-n+1$ 个独立 KVL 方程,可以每选取一个回路时包括一条新的支路。(注意这是选取的充分而非必要条件)
例题预留位
回路电流法
选择 $b-n+1$ 个独立回路,以各回路电流为待求量列写 KVL 方程
一般规则:
$$\begin{bmatrix} R_{11}& R_{12}& \cdots& R_{1m}\\ R_{21}& R_{22}& \cdots& R_{2m}\\ \vdots& \vdots& & \vdots\\ R_{1m}& R_{2m}& \cdots& R_{mm} \end{bmatrix} \begin{bmatrix} I_{m1}\\I_{m2}\\\vdots\\I_{mm}\\ \end{bmatrix}= \begin{bmatrix} \displaystyle \sum_{回路1}U_s\\\displaystyle \sum_{回路2}U_s\\\vdots\\\displaystyle \sum_{回路m}U_s\\ \end{bmatrix} $$
- 组成回路 $i$ 的各支路上电阻之和 $R_{ii}$ 称为回路的自阻
- 回路 $i$ 和回路 $j$ 之间公共支路上的电阻 $R_{ij}$,称为相邻两回路之间的互阻,在公共支路上同向取正、反向取负
- $\displaystyle \sum_{回路i}U_S$ 为沿回路 $i$ 电压源电位升的代数和
- 其中 $(I_{m1},_{m2},\cdots,I_{mm})^T$ 称作回路电流向量,$\begin{pmatrix}\displaystyle \sum_{回路1}U_S,\displaystyle \sum_{回路2}U_S,\cdots,\displaystyle \sum_{回路m}U_S\end{pmatrix}^T$ 称作回路源电压向量
不含受控电源的情况下 $R_{ij}=R_{ji}$,
当电路中包括电流源时,需要先设出电流源两端电压,并补充一个电流源所在支路电流与回路电流的关系。可以适当选取回路使得电流源只包含在一个回路中
当电路中包括受控电源时,先将受控电源当做独立源处理,再将关系代入
例题预留位
节点电压法
任选一节点作为参考点,其它各节点与参考点之间的电压称为该节点的节点电压或节点电位
用节点电压表示支路电压时,相当于等价地列写了 KVL 方程(?)
以 $n-1$ 个节点电压为待求量,对 $n-1$ 个节点列写 KCL 方程的方法就是节点电压法或节点分析法
一般规则:
$$\begin{bmatrix} G_{11}& G_{12}& \cdots& G_{1(n-1)}\\ G_{21}& G_{22}& \cdots& G_{2(n-1)}\\ \vdots& \vdots& & \vdots\\ G_{1(n-1)}& G_{2(n-1)}& \cdots& G_{(n-1)(n-1)} \end{bmatrix} \begin{bmatrix} U_{n1}\\U_{n2}\\\vdots\\U_{nn}\\ \end{bmatrix}= \begin{bmatrix} \displaystyle \sum_{节点1}I_S+\displaystyle \sum_{节点1}G_kU_{Sk}\\ \displaystyle \sum_{节点2}I_S+\displaystyle \sum_{节点2}G_kU_{Sk}\\ \vdots\\ \displaystyle \sum_{节点(n-1)}I_S+\displaystyle \sum_{节点(n-1)}G_kU_{Sk}\\ \end{bmatrix} $$
- 与节点 $i$ 相连的各支路电导之和 $G_{ii}$ 称为该节点的自导
- 直接连接在节点 $i$ 和节点 $j$ 之间各支路电导之和取相反数 $G_{ij}$ 称为节点 $i,j$ 之间的互导
- $\displaystyle \sum_{节点i}I_S$ 为与节点 $i$ 相连的电流源电流代数和(流入取正,流出取负);$\displaystyle \sum_{节点i}G_kU_{Sk}$ 是与节点 $i$ 相连的电压源与串联电导乘积的代数和(电压源正极性指向节点时取正,否则取负)
- 其中 $\begin{pmatrix}U_{n1},U_{n2},\cdots,U_{nn}\end{pmatrix}^T$ 称为节点电压向量,等式右边称为节点源电流向量
改进节点电压法
(我还没研究,之后再填)
例题预留位
电路等效
注意:等效只针对外部电路而言,不包括内部电路,意味着变换前后内部电路的参数(电压、电流、功率等)会发生变化
电阻网络(无源二端网络)
这里就是指里面连了一大坨电阻,本部分会包括一些我自己总结的例子
- 以下两种形式等效(并联 + 串联)
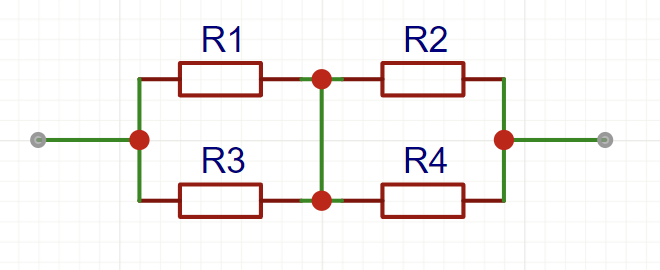
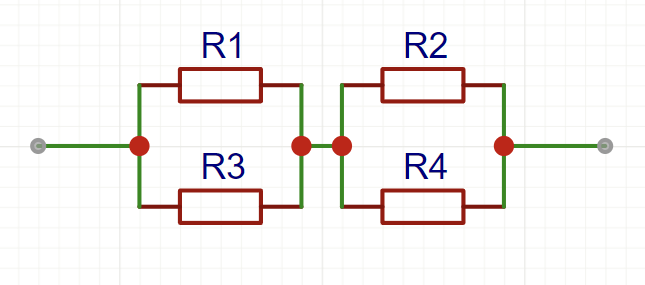
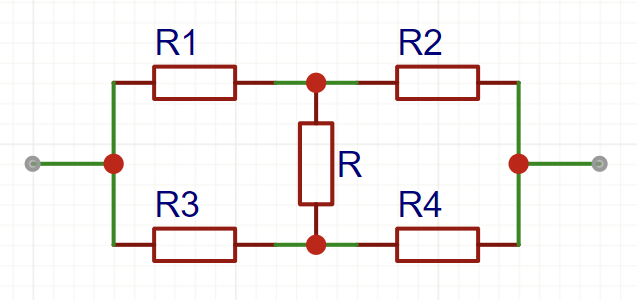
- 以下电路,当 $\displaystyle\frac{R_1}{R_2}=\frac{R_3}{R_4}$ 时,中间的电桥 $R$ 可以直接改为断路
- $Y$ 形联结(左)和 $\Delta$ 形联结(右)
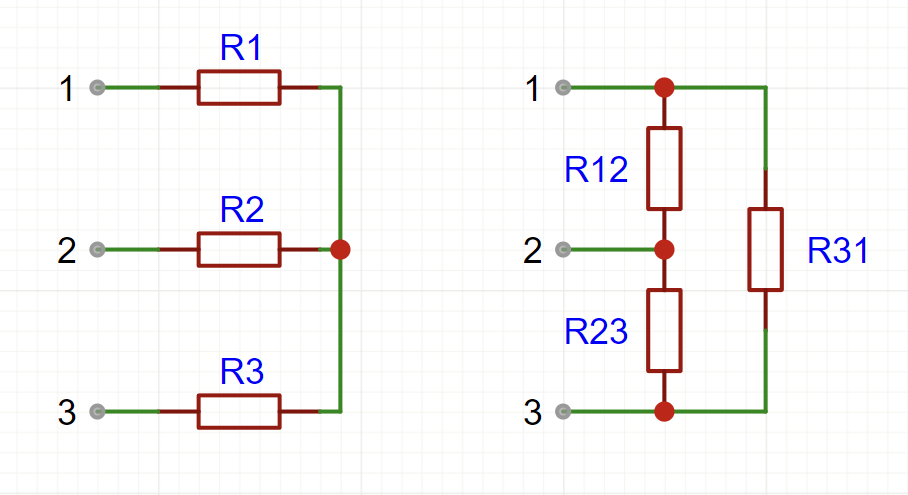
两种联结之间的等效关系式为
$$\begin{aligned} &\left\{ \begin{aligned} R_1=\frac{R_{12}R_{31}}{R_{12}+R_{23}+R_{31}}\\ R_2=\frac{R_{12}R_{23}}{R_{12}+R_{23}+R_{31}}\\ R_3=\frac{R_{23}R_{31}}{R_{12}+R_{23}+R_{31}} \end{aligned} \right.& R_{1,2,3}=\frac{\Delta 形联结中与该节点相连的两电阻之积}{\Delta 形联结中各电阻之和} \\\\ &\left\{ \begin{aligned} R_{12}=\frac{R_{1}R_{2}+R_{2}R_{3}+R_{3}R_{1}}{R_3}\\ R_{23}=\frac{R_{1}R_{2}+R_{2}R_{3}+R_{3}R_{1}}{R_1}\\ R_{31}=\frac{R_{1}R_{2}+R_{2}R_{3}+R_{3}R_{1}}{R_2} \end{aligned} \right.& R_{12,23,31}=\frac{Y 形联结中各电阻两两乘积之和}{Y 形联结中不相邻电阻} \end{aligned} $$
一般用对称情况 $R_1=R_2=R_3=R_Y$,$R_{12}=R_{23}=R_{31}=R_{\Delta}$,其中 $R_{\Delta}=3R_Y$
含源支路的等效变换
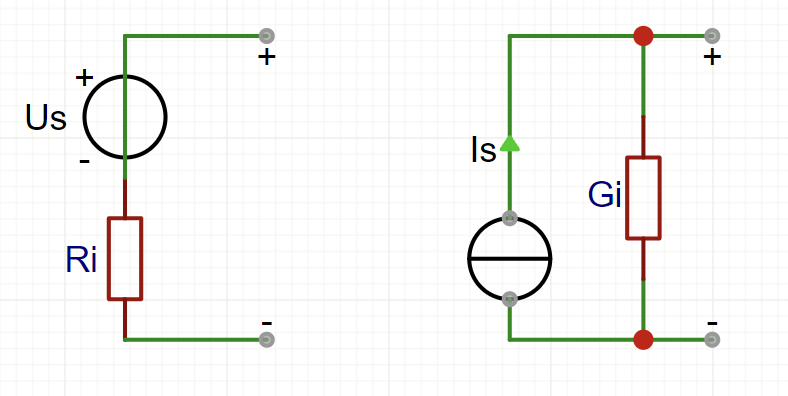
变换条件
$$U_S=\frac{I_S}{G_i},R_i=\frac{1}{G_i} $$
其中 $R_i\neq0,G_i\neq0$(否则为理想电压 / 电流源)
等效电源(戴维南定理 & 诺顿定理)
戴维南定理 线性含源端口网络对外作用可以用一个电压源串联一个电阻的电路来等效替代,其中
- 电压源的源电压等于此端口网络的开路电压(去阻留源)
- 电阻等于此一端口网络内部各独立源置零后所得无源一端口网络的等效电阻(去源留阻)
诺顿定理 线性含源端口网络对外作用可以用一个电流源并联一个电导的电路来等效替代,其中
- 电流源的源电流等于此端口网络的短路电压
- 电导等于此一端口网络内部各独立源置零后所得无源一端口网络的等效电导
